pytorch0.4的概述

Posted on | In
Words count in article: 1,877 字 | Reading time ≈ 9 分钟

pytorch0.4支持了Windows系统的开发，在首页即可使用pip安装pytorch和torchvision。
说白了，以下文字就是来自官方文档60分钟入门的简要翻译.

pytorch是啥

python的科学计算库，使得NumPy可用于GPU计算，并提供了一个深度学习平台使得灵活性和速度最大化

入门

Tensors(张量)

Tensors与NumPy的ndarrays类似，另外可以使用GPU加速计算

未初始化的5*3的矩阵:x = torch.empty(5, 3)
随机初始化的矩阵:x = torch.rand(5, 3)
全零矩阵,定义数据类型:x = torch.zeros(5, 3, dtype=torch.long)
由数据构造矩阵:x = torch.tensor([5.5, 3])
由已存在张量构造矩阵，性质与之前张量一致:

1
2
x = x.new_ones(5, 3, dtype=torch.double) 
x = torch.randn_like(x, dtype=torch.float)

获取维度:print(x.size())

Operations

有多种operation的格式，这里考虑加法

1.

1
2
y = torch.rand(5, 3)
print(x + y)

2.

1
print(torch.add(x, y))

3.

1
2
3
result = torch.empty(5, 3)
torch.add(x, y, out=result)
print(result)

4.

1
2
3
# adds x to y
y.add_(x)
print(y)

operations中需要改变张量本身的值，可以在operation后加,比如`x.copy(y), x.t_()`

索引:print(x[:, 1])
改变维度:x.view(-1, 8)

和Numpy的联系

torch tensor 和 numpy array之间可以进行相互转换，他们会共享内存位置，改变一个，另一个会跟着改变。

tensor to array

1
2
3
4
a = torch.ones(5)
b = a.numpy()
a.add_(1)
print(a,b)

array to tensor

1
2
3
4
5
6
import numpy as np
a = np.ones(5)
b = torch.from_numpy(a)
np.add(a, 1, out=a)
print(a)
print(b)

CUDA Tensors

tensor可以使用.to方法将其移动到任何设备。

1
2
3
4
5
6
7
8
9
# let us run this cell only if CUDA is available
# We will use ``torch.device`` objects to move tensors in and out of GPU
if torch.cuda.is_available():
    device = torch.device("cuda")          # a CUDA device object
    y = torch.ones_like(x, device=device)  # directly create a tensor on GPU
    x = x.to(device)                       # or just use strings ``.to("cuda")``
    z = x + y
    print(z)
    print(z.to("cpu", torch.double))       # ``.to`` can also change dtype together!

Autograd(自动求导)

pytorch神经网络的核心模块就是autograd，autograd模块对Tensors上的所有operations提供了自动求导。

Tensor

torch.Tensor是模块中的核心类，如果设置属性.requires_grad = True,开始追踪张量上的所有节点操作，指定其是否计算梯度。使用.backward()方法进行所有梯度的自动求导，张量的梯度会累积到.grad属性中。
.detach()停止张量的追踪，从梯度计算中分离出来；另外在评估模型时一般使用代码块with torch.no_grad():,因为模型中通常训练的参数也会有.requires_grad = True,这样写可以停止全部张量的梯度更新。
Function类是autograd的变体，Tensor和Function相互交错构建成无环图，编码了完整的计算过程，每个Variable(变量)都有.grad_fn属性，引用一个已经创建了的Tensor的Function.
如上，使用.backward()计算梯度。如果张量是一个标量(只有一个元素),不需要对.backward()指定参数；如果张量不止一个元素，需要指定.backward()的参数，其匹配张量的维度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import torch
x = torch.ones(2, 2, requires_grad=True)
print(x)
y = x + 2
print(y)
print(y.grad_fn)
z = y * y * 3
out = z.mean()
print(z, out)

a = torch.randn(2, 2)
a = ((a * 3) / (a - 1))
print(a.requires_grad)
a.requires_grad_(True) # 改变a张量内在的属性
print(a.requires_grad)
b = (a * a).sum()
print(b.grad_fn)

Gradients

反向传播时，由于out是一个标量，out.backward()等效于out.backward(torch.tensor(1))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
out.backward()
print(x.grad)

x = torch.randn(3, requires_grad=True)

y = x * 2
while y.data.norm() < 1000:
    y = y * 2

print(y)

gradients = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float)
y.backward(gradients)

print(x.grad)

print(x.requires_grad)
print((x ** 2).requires_grad)

with torch.no_grad():
    print((x ** 2).requires_grad)

神经网络

神经网络可以用torch.nn构建。nn依赖于autograd定义模型和求导，nn.Module定义网络层，方法forward(input)返回网络输出。

举例说明，如下是对数字图片分类的卷积网络架构。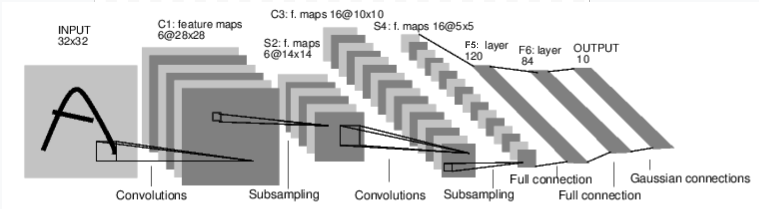

这是一个简单的前馈神经网络，将输入数据依次通过几层网络层后最终得到输出。
神经网络典型的训练步骤如下：

  • 定义神经网络及学习的参数(权重)
  • 迭代输入数据
  • 将输入数据输入到网络结构中
  • 计算代价函数
  • 误差向后传播
  • 更新网络权重 weight = weight - learning_rate * gradient

定义网络

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
import torch
import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        # 1 input image channel, 6 output channels, 5x5 square convolution
        # kernel
        self.conv1 = nn.Conv2d(1, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # Max pooling over a (2, 2) window
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # If the size is a square you can only specify a single number
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

    def num_flat_features(self, x):
        size = x.size()[1:]  # all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
        return num_features


net = Net()
print(net)

out:

1
2
3
4
5
6
7
Net(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

可以仅定义forward()函数，当使用autograd时backward()被自动定义。可以在forward()函数中使用任何operation操作。
net.parameters()返回模型中的可学习参数。

1
2
3
params = list(net.parameters())
print(len(params))
print(params[0].size())  # conv1's .weight

使所有参数的梯度归零然后开始计算梯度

1
2
net.zero_grad()
out.backward(torch.randn(1, 10))

代价函数

代价函数将(output,target)作为输入，计算output与target之间的距离。
nn模块中有几种不同的代价函数选择，最简单的是nn.MSELoss，计算均方误差
eg：

1
2
3
4
5
6
7
output = net(input)
target = torch.arange(1, 11)  # a dummy target, for example
target = target.view(1, -1)  # make it the same shape as output
criterion = nn.MSELoss()

loss = criterion(output, target)
print(loss)

按照向后传播的方向传播loss，使用grad_fn可以查看整个流程的计算图

1
2
3
4
input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d
      -> view -> linear -> relu -> linear -> relu -> linear
      -> MSELoss
      -> loss

使用loss.backward()，流程中所有requres_grad=True的张量累积它的梯度至.grad

1
2
3
print(loss.grad_fn)  # MSELoss
print(loss.grad_fn.next_functions[0][0])  # Linear
print(loss.grad_fn.next_functions[0][0].next_functions[0][0])  # ReLU

向后传播

loss.backward()传播误差，

1
2
3
4
5
6
7
8
9
net.zero_grad()     # zeroes the gradient buffers of all parameters

print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)

loss.backward()

print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)

更新权重

误差每次传播后，需要对权重进行更新，简单的更新方式如下：

1
2
3
learning_rate = 0.01
for f in net.parameters():
    f.data.sub_(f.grad.data * learning_rate)

torch.optim实现了这一过程，并有着不同的更新规则GD, Nesterov-SGD, Adam, RMSProp，

1
2
3
4
5
6
7
8
9
10
11
import torch.optim as optim

# create your optimizer
optimizer = optim.SGD(net.parameters(), lr=0.01)

# in your training loop:
optimizer.zero_grad()   # zero the gradient buffers
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()    # Does the update

note: 每次迭代时由于梯度的累积，需要手动将梯度归零optimizer.zero_grad()